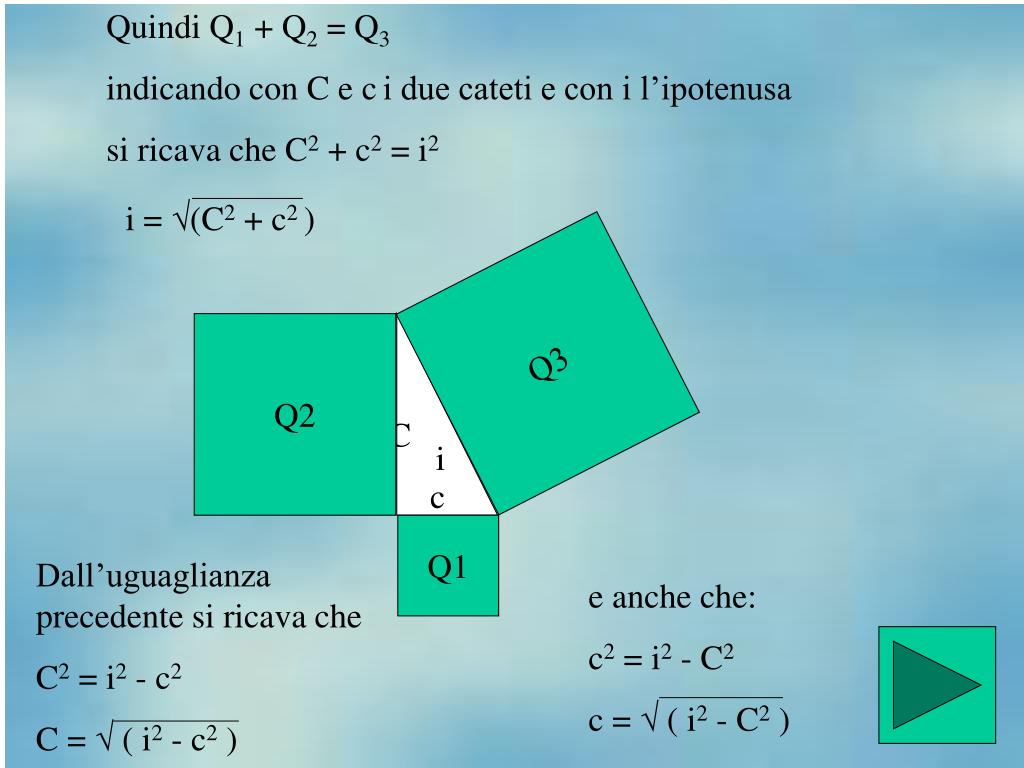
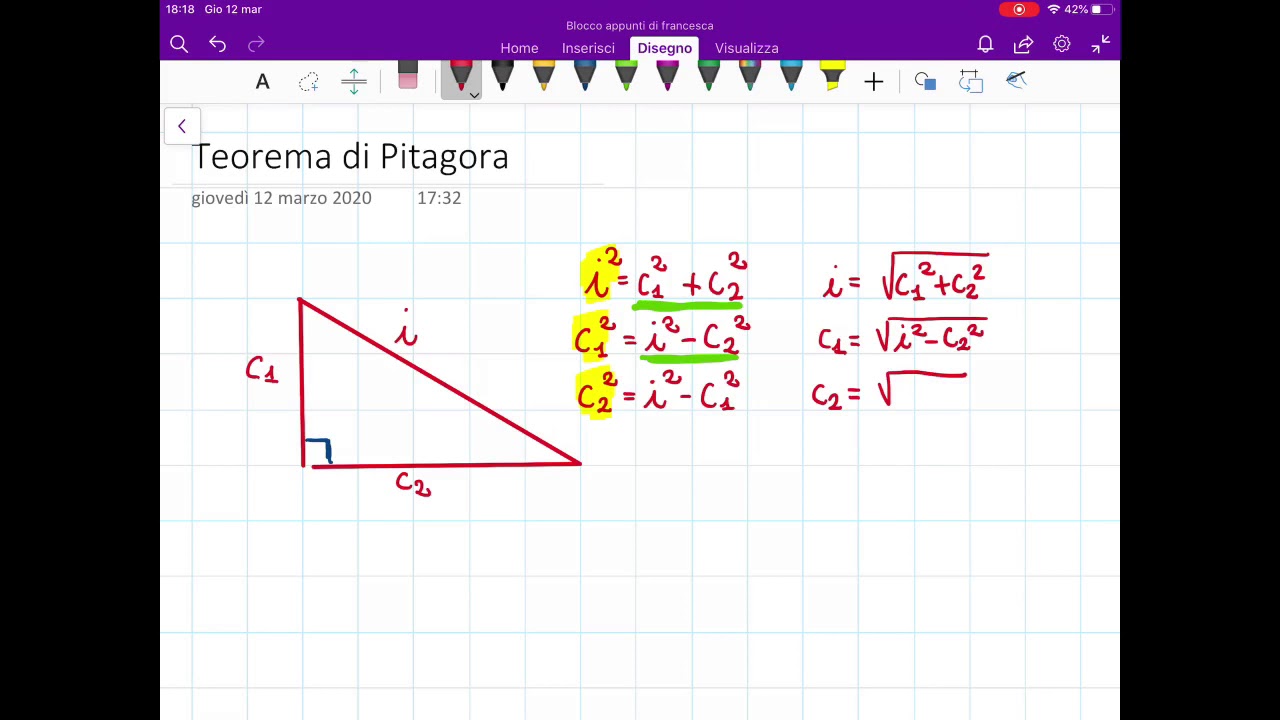
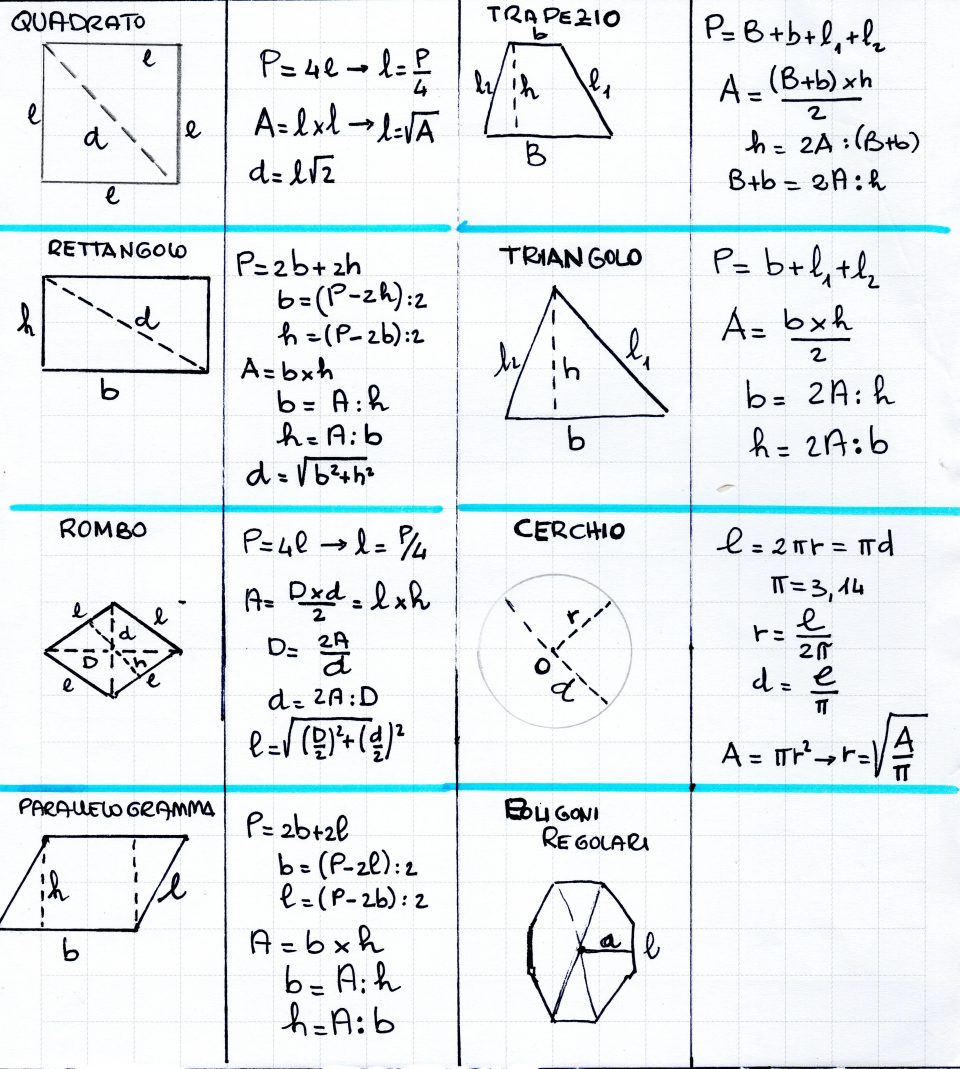
Il teorema di Pitagora: enunciato, formule e dimostrazione. Uno dei teoremi più famosi di tutta la Geometria Euclidea è il teorema di Pitagora. Esso afferma che il quadrato costruito sull'ipotenusa di un triangolo rettangolo è equivalente alla somma dei quadrati costruiti sui cateti del triangolo considerato.. Di conseguenza, se conosciamo l'altezza e la base del triangolo isoscele e vogliamo trovare il suo lato, potremo utilizzare il teorema di Pitagora e scrivere: Come formule inverse avremo: Esempio: calcolare il perimetro di un triangolo isoscele la cui altezza misura m 4 e il cui lato obliquo misura m 6.
PPT TEOREMA DI PITAGORA PowerPoint Presentation, free download ID5264201
Il Teorema Di Pitagora Introduzione YouTube

2.4 Teorema di Pitagora nel rettangolo YouTube

Il Teorema Di Pitagora 2ª Media Teorema di pitagora, Matematica scuola

Teorema di Pitagora YouTube

Problemi Teorema di Pitagora Mauitaui e la matematica

Terne pitagoriche e inverso del teorema di Pitagora per Medie Redooc

15. Triangoli speciali Teorema di pitagora, Matematica scuola media, Scuola media

11. Teorema di Pitagora Teorema di pitagora, Scuola media, Matematica scuola media

TEOREMA di PITAGORA e ROMBO lezioniignoranti
RIPASSIAMO IL TEOREMA DI PITAGORA lezioniignoranti
Teorema di Pitagora applicato al triangolo isoscele

Calaméo IL TEOREMA DI PITAGORA

Il teorema di Pitagora YouTube

Le formule del Teorema di Pitagora YouTube

Formule Teorema di Pitagora per Medie Redooc
Il teorema di Pitagora applicato al rombo esempio 2

RIPASSIAMO IL TEOREMA DI PITAGORA lezioniignoranti

la breda in rete 2A Pitagora le formule

Formule del Teorema di Pitagora YouTube
Semplicemente applichiamo la formula del teorema di Pitagora: dove. c = cateto minore = 4 cm. C = cateto maggiore = 5 cm. i = √ (4^2+5^2)=√ (9+16)=√25. i=5. Esempio 2) Dato il triangolo isoscele di perimetro 64 cm e base 24 cm. Calcolare l'area del triangolo. Poiché il triangolo isoscele ha due lati uguali possiamo riscrivere la.. Ecco come utilizzare il teorema di Pitagora: Inserisci nella formula le due lunghezze di cui disponi. Ad esempio, supponiamo di conoscere il cateto a = 4 e l'ipotenusa c = 8,94.Vogliamo trovare la lunghezza dell'altro cateto b.; Dopo aver inserito i valori nella formula, otteniamo 4² + b² = 8,94².; Calcolati i quadrati, otteniamo 16 + b² = 80²..