正多面体やオイラーの多面体定理について理解しましょう。 多面体. . 多面体 とは，いくつかの平面で囲まれた立体のことです。 直方体や四面体など，小学生の頃から色んな多面体を学習してきました。 一方，円錐や球は多面体ではありません。 平面のみならず，曲面を含む立体だからですね。 次のような立体も多面体です。 平面に囲まれてできていますね。 このように凹みのない立体を 凸多面体 といいます。 次のように凹みがある立体は凹多面体といいますが，学校ではあまり扱いません。 ここでも主に凸多面体について考えることにします。 オイラーの多面体定理. . . 凸多面体の頂点（ vertex ），辺（ edge ），面（ face ）の数について，次の定理が成り立ちます。 オイラーの多面体定理.. 正多面体 面・頂点・辺の数. Googleで「 正多面体 」（最後はスペースね）と入力すると、Google先生が教えてくれるリストの先頭が「展開図」。. あれ？. 今年の3月には「証明」だったよ～. 今は「証明」がサジェストリストに出てこない!. （2012/12/22.

正多面体が5種類しかないことの2通りの証明 高校数学の美しい物語

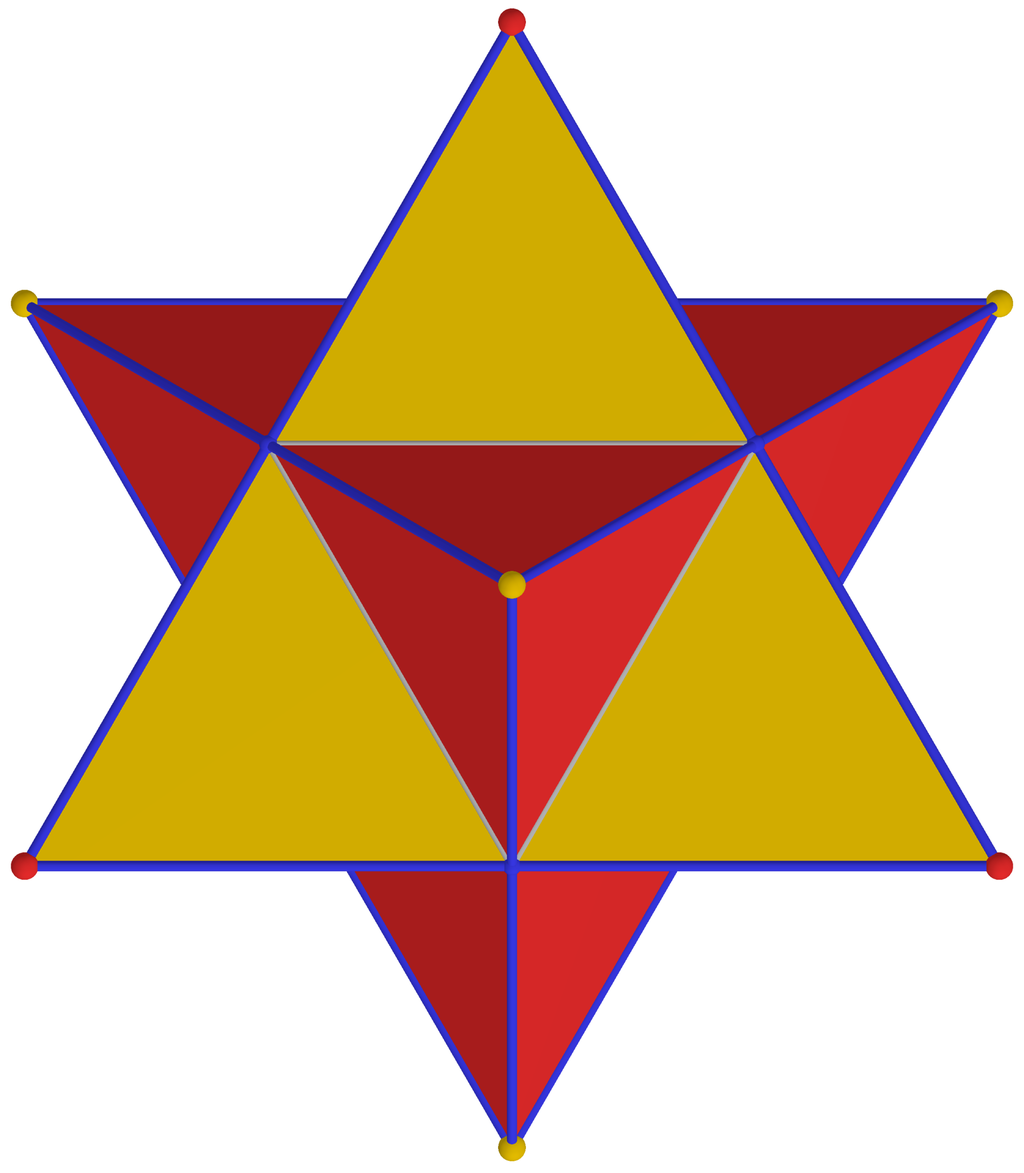
正多面体の辺と面の数の覚え方 ばたぱら

数学A 図形の性質[オイラーの多面体定理]問題 YouTube

正多面体の辺と頂点の数 ｜ 久保塾 今治市の学習塾 小学生・中学生・高校生・大学受験

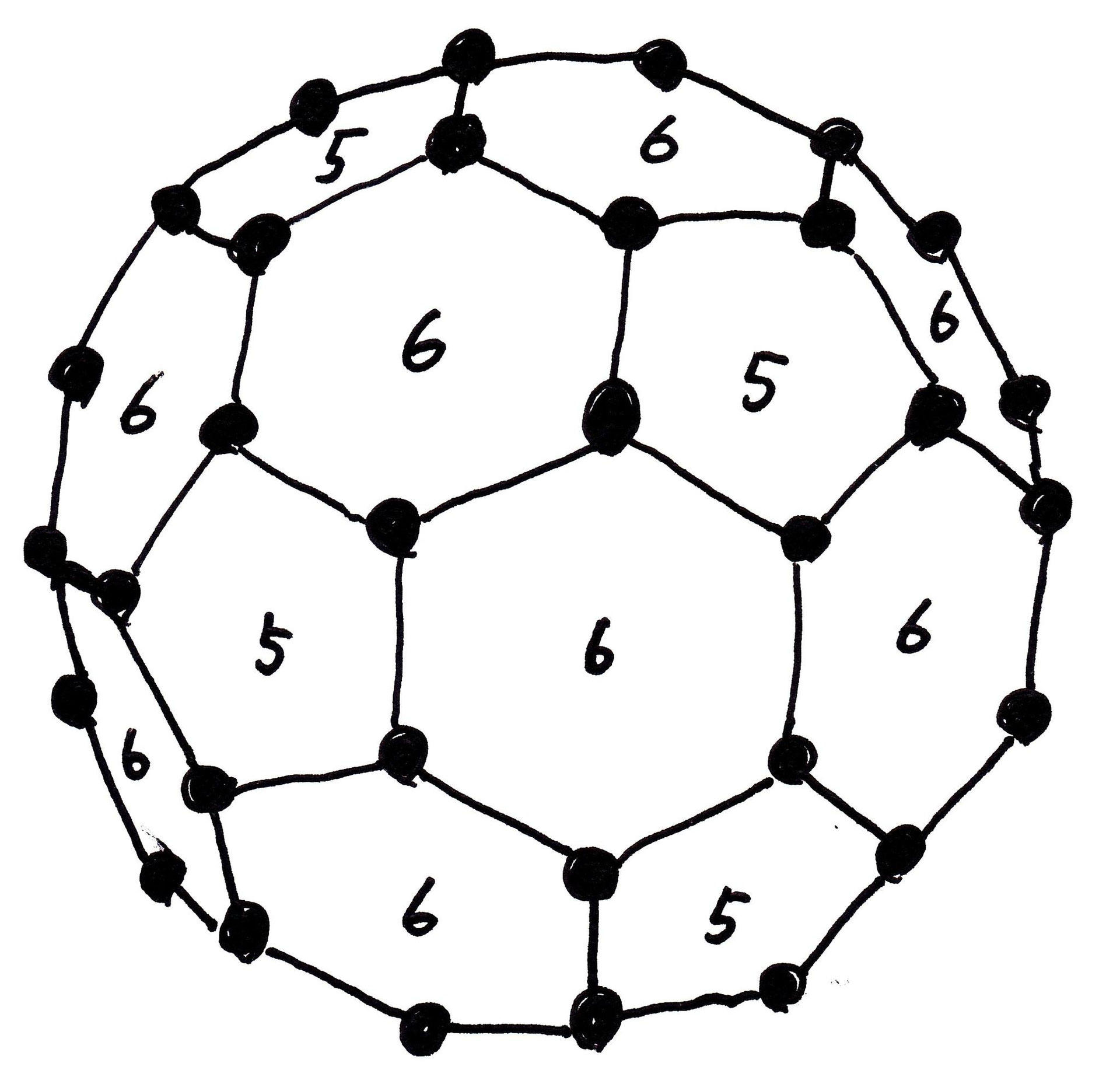
正多面体の頂点と辺の数を求める しもまっちハイスクール

高校入試[英語・数学]学習｜正多面体

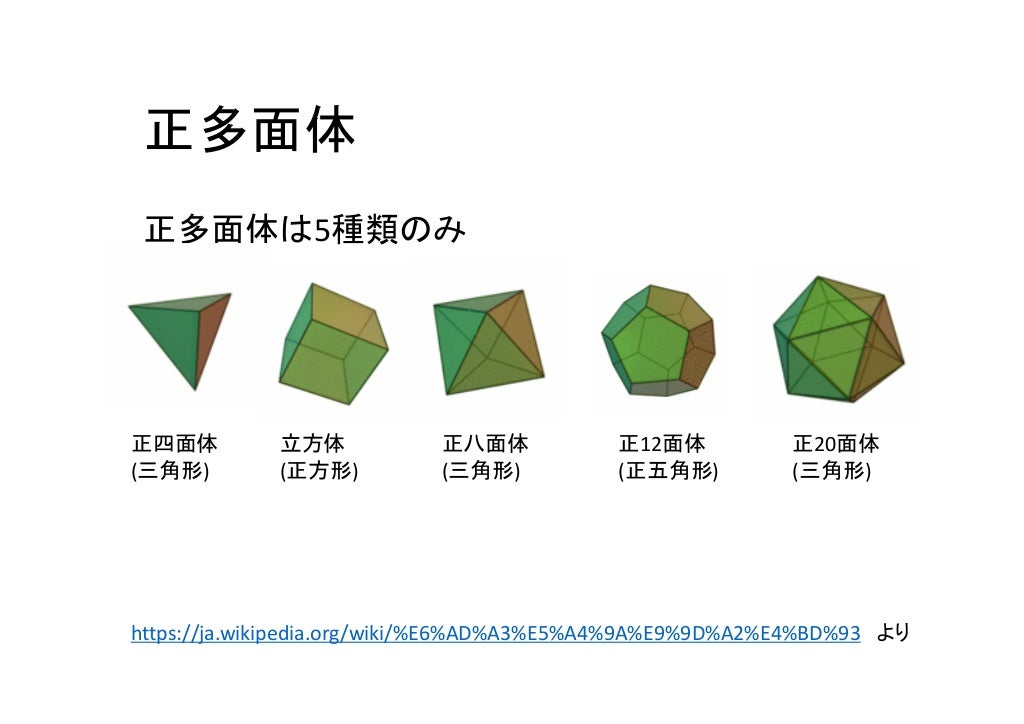
正多面体と展開図

正多面体の辺と面の数の覚え方 ばたぱら

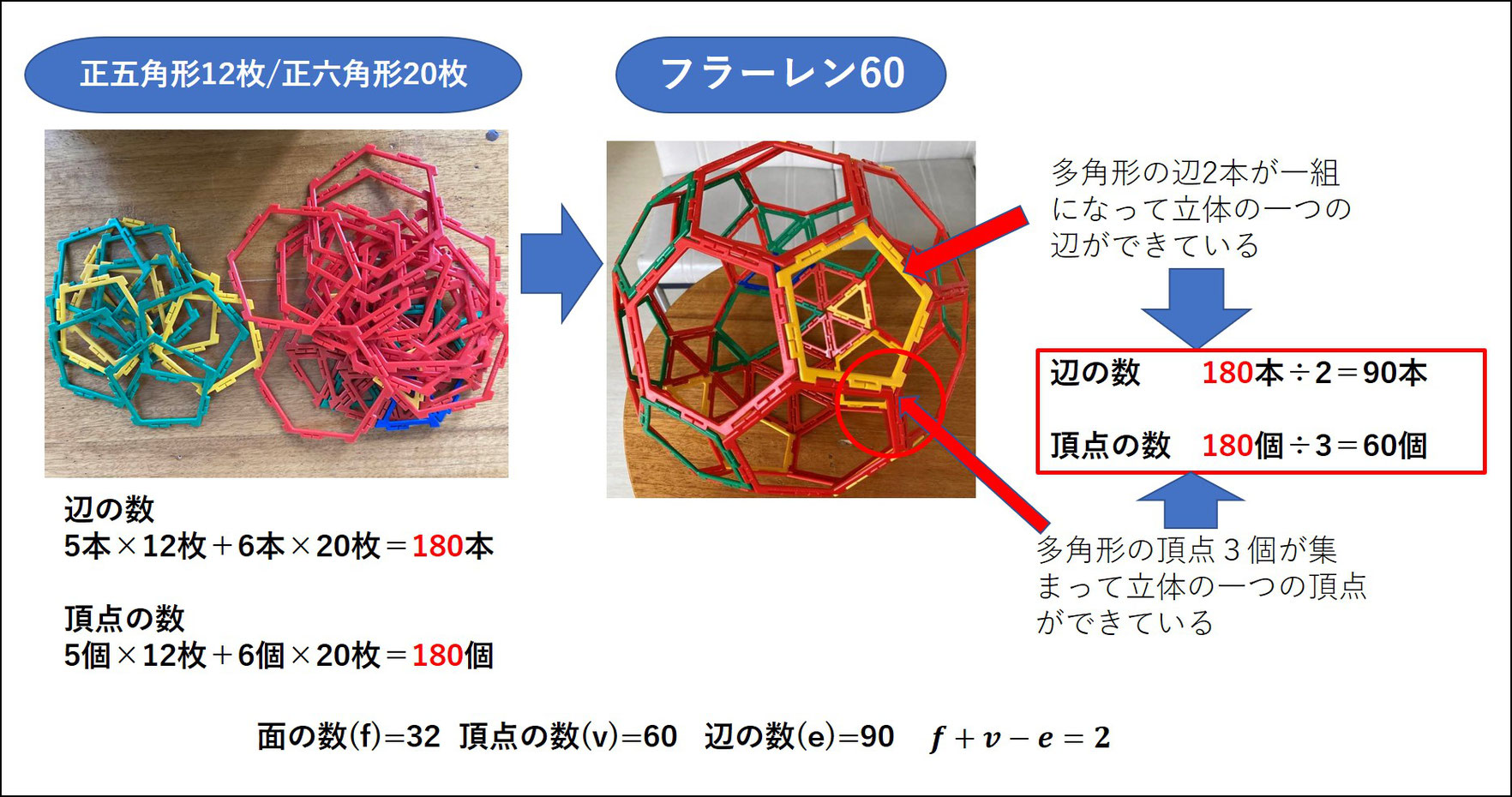
正多面体の頂点と辺の数を求める しもまっちハイスクール

おうちで算数工作！正多面体5種類の展開図データを無料公開します！｜math channel

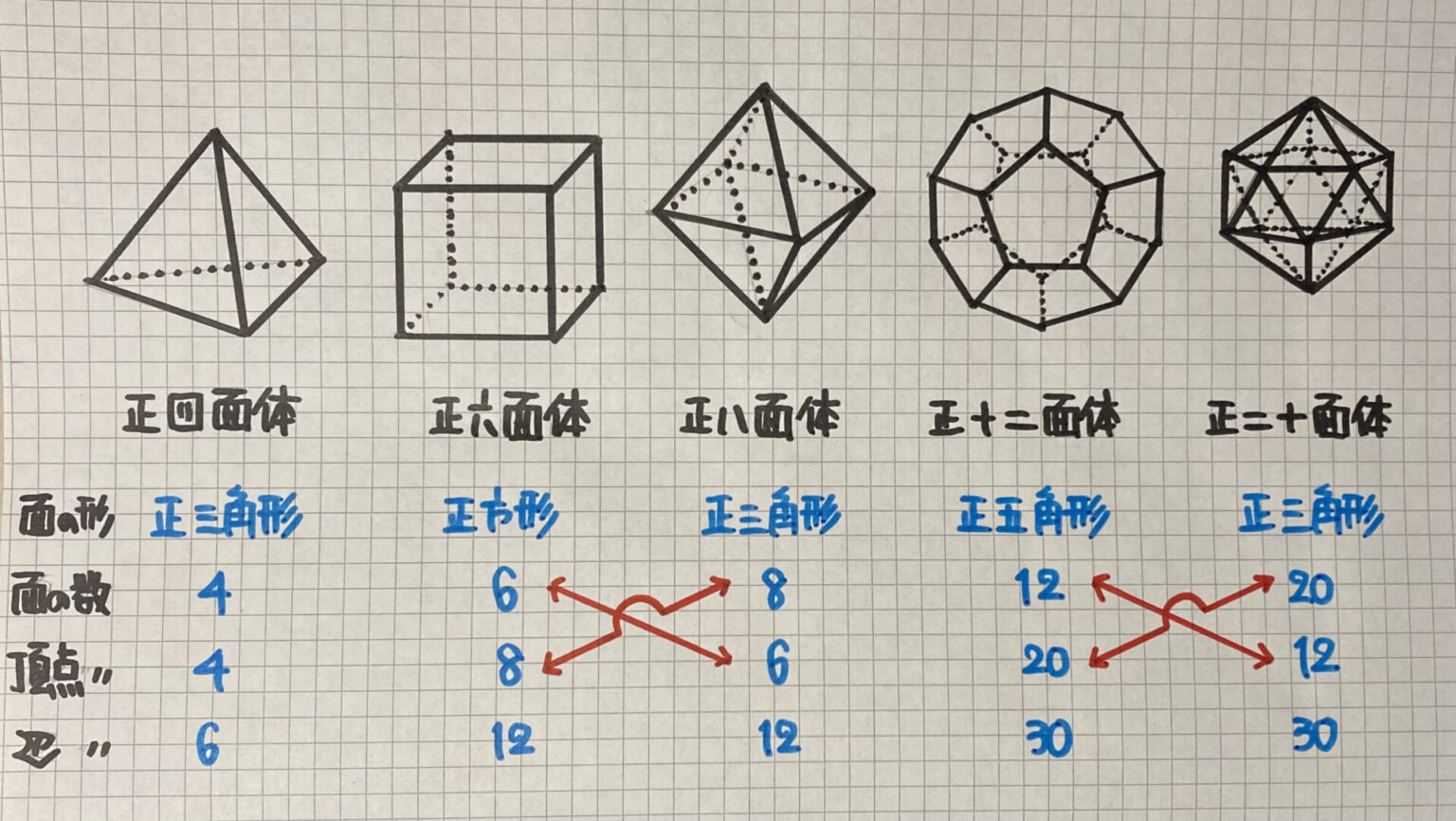
【中1数学】「いろいろな立体」の問題 どこよりも簡単な解き方・求め方｜かずのかずブログ

正多面体 ＜数学＞ さくら教育研究所（SKREDU）

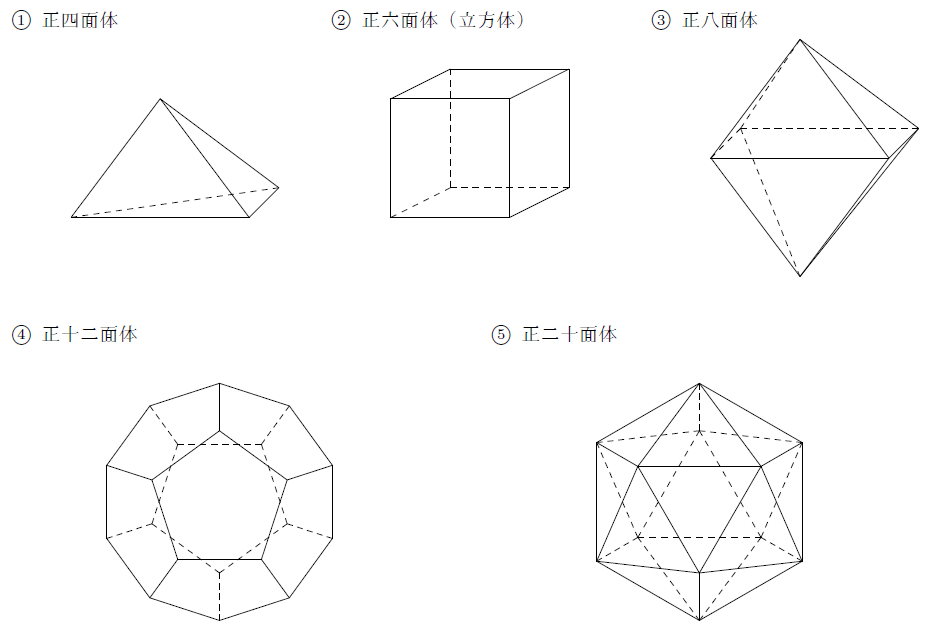
【講義】多面体 まなびの学園

【高校数学A】「正多面体とは？」(練習編) 映像授業のTry IT (トライイット)

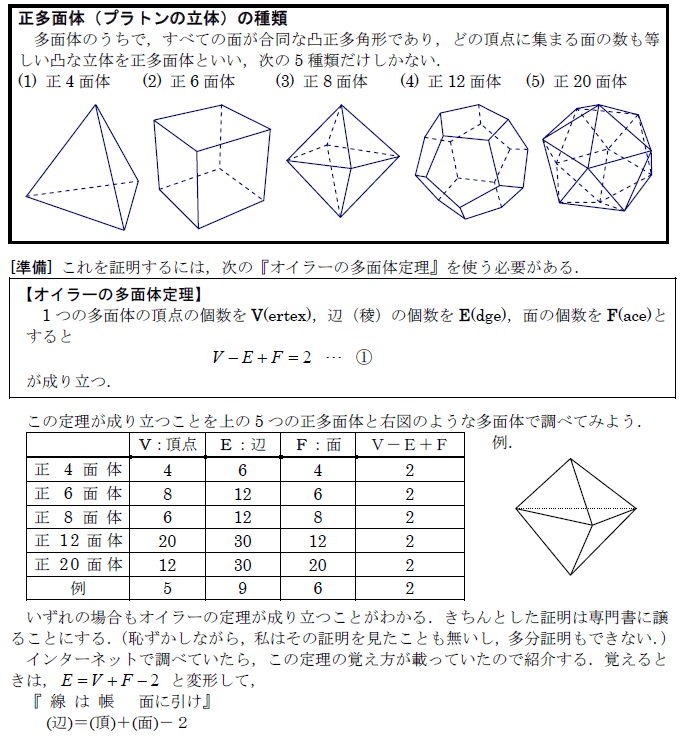
オイラーの多面体定理 入試問題の攻略法 （さくら教育研究所）（SKREDU）

【中1数学】 空間図形 正多面体② ～ 正多面体の 辺の数 と 頂点の数 ～ (完全版) YouTube

【正多面体が100均に！】頂点の数・辺の数の理解補助に 東大和の個別指導塾フォーラムステーション 基導会進学スクール

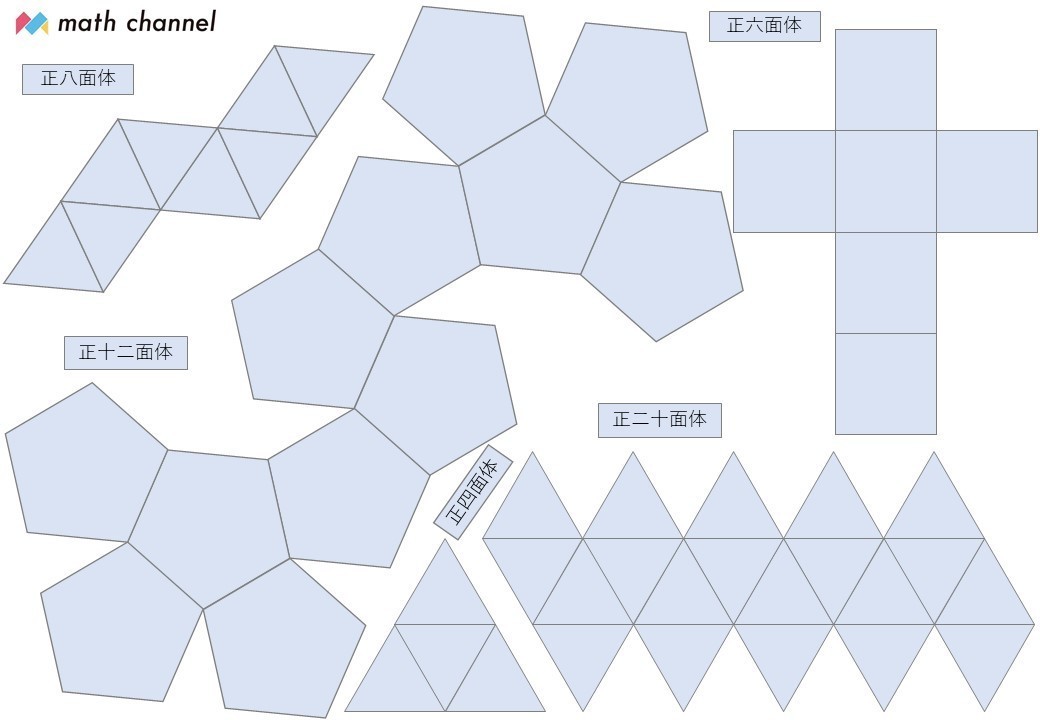
おうちで算数工作！正多面体5種類の展開図データを無料公開します！｜math channel｜note

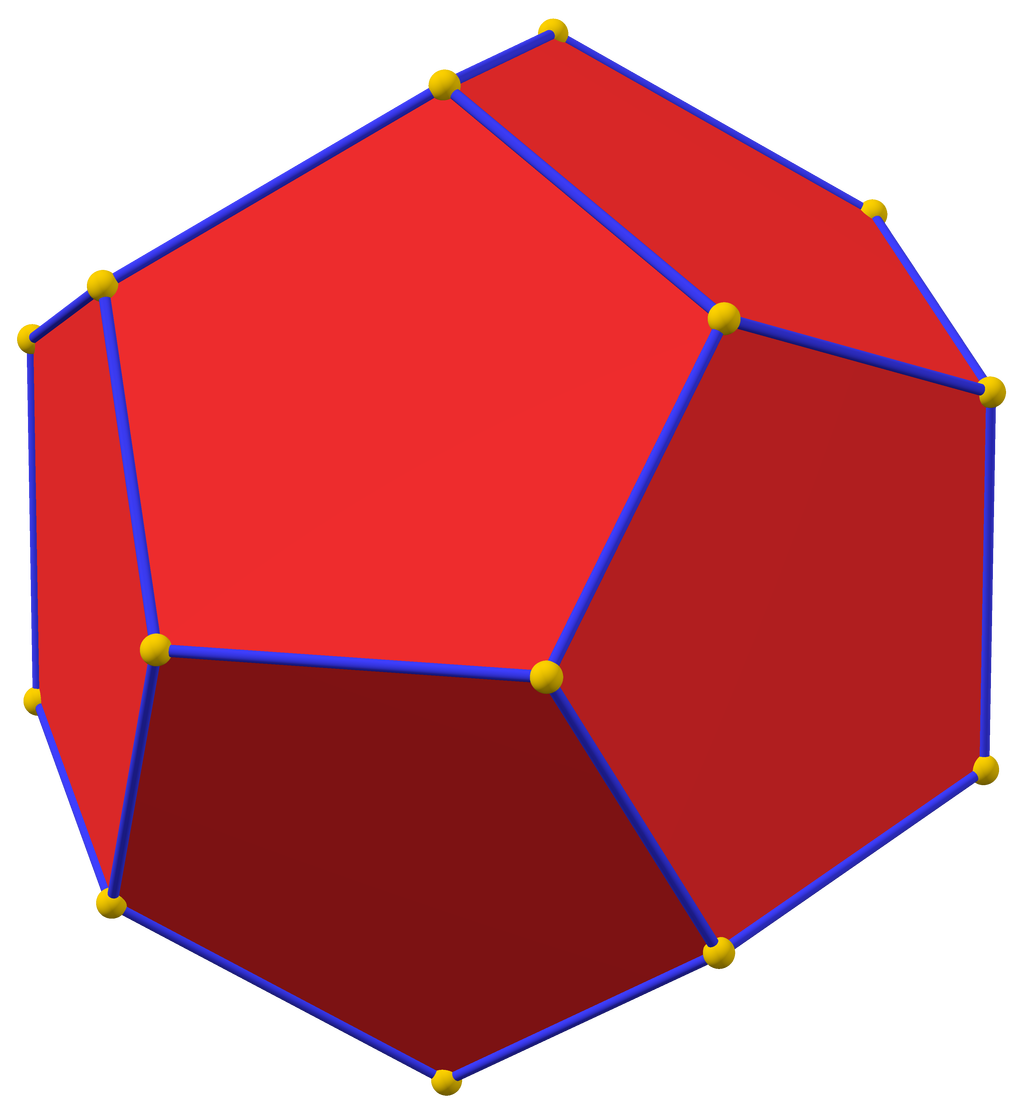
正多面体の辺と面の数の覚え方 ばたぱら

【正多面体が100均に！】頂点の数・辺の数の理解補助に 東大和の個別指導塾フォーラムステーション 基導会進学スクール

高校数学Aで学習する図形の性質の単元から「正多面体の面、頂点、辺の数」についてイチから解説しています。 ★講義資料はこちらから★＞https://bit.ly/3M8U3gh 数スタのサイトはこちら＞https://study-line.com/00:00 今回の問題00:17 表を埋めるためのポイント02:51.. 正多面体の性質とオイラーの多面体定理. 凸多面体 多面体のうち,\ どの2つの頂点を結んだ線分もその多面体内に含まれるもの. 凸多面体の頂点 (Vertex),\ 辺 (Edge),\ 面 (Face)の数をそれぞれ$V,\ E,\ F$とする. このとき,\ オイラーの多面体定理 (暗記必須)が.